基础优化-最不坏的哈希表
哈希表性能优化的方法有很多,比如:
- 使用双 hash 检索冲突
- 使用开放+封闭混合寻址法组织哈希表
- 使用跳表快速定位冲突
- 使用 LRU 缓存最近访问过的键值,不管表内数据多大,短时内访问的总是那么几个
- 使用更好的分配器来管理 key_value_pair 这个节点对象
上面只要随便选两条你都能得到一个比 unordered_map 快不少的哈希表,类似的方法还有很多,比如使用除以质数来归一化哈希值(x86下性能最好,整数除法非常快,但非x86就不行了,arm还没有整数除法指令,要靠软件模拟,代价很大)。
哈希表最大的问题就是过分依赖哈希函数得到一个正态分布的哈希值,特别是开放寻址法(内存更小,速度更快,但是更怕哈希冲突),一旦冲突多了,或者 load factor 上去了,性能就急剧下降。
Python 的哈希表就是开放寻址的,速度是快了,但是面对哈希碰撞攻击时,挂的也是最惨的,早先爆出的哈希碰撞漏洞,攻击者可以通过哈希碰撞来计算成千上万的键值,导致 Python / Php / Java / V8 等一大批语言写成的服务完全瘫痪。
后续 Python 推出了修正版本,解决方案是增加一个哈希种子,用随机数来初始化它,这都不彻底,开放寻址法对hash函数的好坏仍然高度敏感,碰到特殊的数据,性能下降很厉害。
经过最近几年的各种事件,让人们不得不把目光从“如何实现个更快的哈希表”转移到 “如何实现一个最不坏的哈希表”来,以这个新思路重新思考 hash 表的设计。
哈希表定位主要靠下面一个操作:
index_pos = hash(key) % index_size;
来决定一个键值到底存储在什么地方,虽然 hash(key) 返回的数值在 0-0xffffffff 之前,但是索引表是有大小限制的,在 hash 值用 index_size 取模以后,大量不同哈希值取模后可能得到相同的索引位置,所以即使哈希值不一样最终取模后还是会碰撞。
第一种思路是尽量避免冲突,比如双哈希,比如让索引大小 index_size 保持质数式增长,但是他们都太过依赖于哈希函数本身;所以第二种思路是把注意力放在碰撞发生了该怎么处理上,比如多层哈希,开放+封闭混合寻址法,跳表,封闭寻址+平衡二叉树。
优化方向
今天我们就来实现一下最后一种,也是最彻底的做法:封闭寻址+平衡二叉树,看看最终性能如何?能否达到我们的要求?实现起来有哪些坑?其原理简单说起来就是,将原来封闭寻址的链表,改为平衡二叉树:
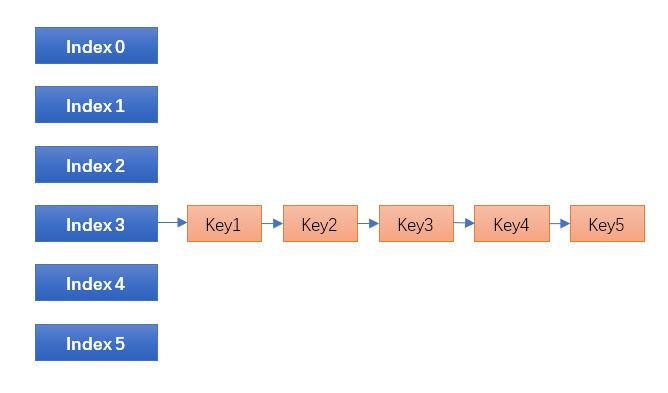
传统的封闭寻址哈希表,也是 Linux / STL 等大部分哈希表的实现,碰到碰撞时链表一长就挂掉,所谓哈希表+平衡二叉树就是:
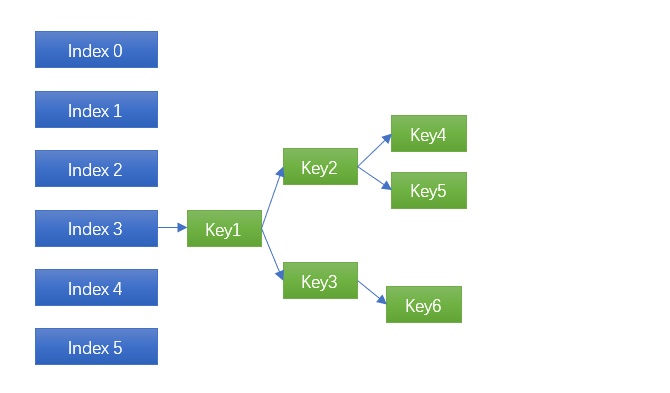
将原来的链表(有序或者无序)换成平衡二叉树,这是复杂度最高的做法,同时也是最可靠的做法。发生碰撞时能将时间复杂度由 O(N) 降低到 O(logN),10个节点,链表的复杂度就是 10,而使用平衡二叉树的复杂度是 3;100个节点前者的时间是100,后者只有6.6 越往后差距约明显。
面临问题
树表混合结构(哈希表+平衡二叉树)的方法,Hash table - Wikipedia 上面早有说明,之所以一直没有进入各大语言/SDK的主流实现主要有四个问题:
- 比起封闭寻址(STL,Java)来讲,节点少时,维持平衡(旋转等)会比有序链表更慢。
- 比起开放寻址(python,v8实现)来讲,内存不紧凑,缓存不够友好。
- 占用更多内存:一个平衡二叉树节点需要更多指针。
- 设计比其他任何哈希表都要复杂。
所以虽然早就有人提出,但是一直都是一个边缘方法,并未进入主流实现。而最近两年随着各大语言暴露出来的各种哈希碰撞攻击,和原有设计基本无力应对坏一些的情况,于是又开始寻求这种树表混合结构是否还有优化的空间。
先来解决第一个问题,如果二叉树节点只有3-5个,那还不如使用有序链表,这是公认的事实,Java 8 最新实现的树表混合结构里,引入了一个 TREEIFY_THRESHOLD = 8 的常量,同一个索引内(或者叫同一个桶/slot/bucket内),冲突键值小于 8 的,使用链表,大于这个阈值时当前 index 内所有节点进行树化操作(treeify)。
Java 8 靠这个方法有效的解决了第一个问题和第三个问题,最终代替了原有 java4-7 一直在使用的 HashMap 老实现,那么我们要使用 Java 8 的方法么?
不用,今天我们换种实现。
java 8 经过了反复测试选择了 TREEIFY_THRESHOLD=8 这个阈值,因为它 treeify 的过程的代价是非常大的:
- 要为每个节点重新分配一个 TreeNode ,分配内存过本身就是很大的一个开销。
- 构造二叉平衡树,其维护平衡即便不需要再平衡,进去也是要走一堆逻辑判断。
- 当节点降低到 UNTREEIFY_THRESHOLD=6这个阈值以内,又要把树节点全部删除掉,换回链表去,那如果 index 内节点就在 5-9 之间波动,这就傻了,这是第三项成本。
- 每次插入节点时要判断这是链表还是树,到阈值没有,大家知道这些额外增加的分支都是对 CPU的流水线十分不友好的。
如果我们能想办法不多分配内存(开销最大),那基本上这个阈值可以降低到 4,再此基础上使用更紧凑的搜索代码,在 gcc 那里可以获得更好的优化,现代CPU对小型分支预测的处理都比较完善,x86下还有 cmov 指令解决跳转,树搜索时多用紧凑的三元式:
node = (key < node->key)? node->left : node->right;
最终生成 cmov 的代码是没有分支的,实测新老 gcc,新版本 gcc 生成 cmov指令性能是没有用 cmov 的一倍以上,诸如此类的代码层的优化技巧我们尽量用起来,让这个阈值降低到 2-3 的时候,也就是说传统的有序链表操作已经没有优化余地了,但是通过降低 treeify 过程中再次分配内存的消耗,树维护的消耗,以及提高树的性能,可以把阈值从 8 降低到 4,再通过代码层的优化降低到 2-3,也就是说,最终链表只有在 2-3个节点以内才比树更快,如果做到这一点,那好,我们的故事就变了。
再链表/树的性能对比阈值降低到 2-3个节点后,接下来我们就可以完全抛弃链表,index里面只保留树结构,然后给平衡二叉树增加几条 fast path,让其性能尽量接近链表,比如大部分时候(hash值较为平均),每个 index只有 0-2个节点的时候,我们的这些快速路径就生效了:
- 当某 index 下面节点数为 0 时,要增加一个节点,我们直接更改树的根节点即可,完全跳过后面的各种再平衡逻辑,以及比较逻辑。
- 如果本来有 1 个节点,要增加一个新节点,那么也完全不需要再平衡,一次比较后直接设置成左或者右儿子同样跳过再平衡逻辑。
- 如果是2个节点变3个节点,那同样很简单,把最大和最小节点找出来,放在剩下节点的左右子树即可,同样跳过再平衡。
这样 3个节点以内我们采取一次性直接构造树的方法免去再平衡逻辑,基本上保证了3个节点以内的树操作和链表代价相同,又因为自始至终只有一种节点,避免了 java8 中同节点可能需要两次内存分配的问题,又大大缩小了链表和树的性能差距,只使用树结构,免除了 treeify, untreeify 两道逻辑和开头的判断,最终达到和链表性能差不多的树结构。
指针优化
再看 TreeNode 内容,大家猜猜一个 java.util.HashMap.TreeNode 对象有多少个成员变量?不说不知道,一说吓一跳,整整 9个变量(HashMap.Node 本身有4个对象,其派生类 HashMap.TreeNode 又增加了5个新变量)。还有每次分配一断内存其实都有一个 overhead ,表明这个内存是从哪里分配出来的,释放的时候好找到归还的位置,全部加在一起有 10个变量,变量越多缓存越不集中,每次操作的成本也越大,我没研究过 java 的对象内存布局,就以 C语言为例 10个变量 32位下要占用 40字节的空间,64位下占用更多。
其中关键的一处冗余是 Java 8 下面为每个节点维护了 next, prev 指针,这两个指针何用?遍历哈希表的时候用。大家知道如果节点不维护 next, prev 而遍历哈希表的话,传统遍历法要遍历所有 index,即便一个 index 为空也要走一圈,python就是这么干的,那么在 load factor 比较高的时候,这么做没问题;而 load factor 很低时,也就是说 index 表很大,但是整个 hash表里的节点却很少时,遍历就会跑很多空的 index,效率很低。
所以 java8 里一个 treeify 过后的索引里,所有节点不当放在树里,还同时放到了链表里了,虽然搜索不搜索链表而是直接搜索树,但是每次插入和删除需要同时操作树和链表,来保证遍历的时候可以不跑空节点,这又是一件肯爹的事情。
那么我们可以把 next, prev 省掉么?当然可以,既然我们已经全部都使用平衡二叉树了,本身平衡二叉树就可以方便的遍历而不需要额外的存储,只是这个 index 里的二叉树遍历完了怎么寻找下一个有效节点?很简单,我们把 next, prev 指针加到 index上,让有数据的 index 连在一起,这个 index 内的所有树节点遍历完了后直接跳到下一个有数据的 index 里的节点上去。这样我们把每个节点都有的 next/prev 拿了出来,放到了 index 上面,插入和删除节点都不需要再同时维护树和链表两个结构,仅仅再节点数 0->1, 1->0时需要把 index 移进/移除链表,保证了遍历时不会跑空的 index,同时为每个节点都省掉了两个指针。
内存优化
开放寻址的 hash 表的优势是:省内存+不需要额外分配内存+缓存友好,使用树表混合结构后,内存显然我们是省不了多少了,但是后两个目的却可以想办法达到,在哈希表内按照 load factor 和初始索引大小计算出 rehash 前最多会有多少个节点,然后一次性分配一整块内存,按照 node 的大小切割后放入哈希表内部的 freelist 中,rehash的时候再重新计算分配另外一块整块内存,这样做有三个明显的好处:
- 内存分配/释放,基本是O(1)极速了,消耗基本可以忽略。
- 表内所有节点再内存上都是连续的,缓存十分友好。
- 免去了为每个节点单独分配内存的头部占用(overhead),相当于又省掉了一个指针。
使用该方法进行内存优化过的树表结构,性能得以再次提升。
其他优化
设计一个数据结构,本身就是再做选择,做权衡,选择了树表混合结构,看重的是它的终极平衡特性,而上面所有工作,其实都是在死磕它的短处,各处可以优化的细节还很多:
比如 rehash 删除原有二叉平衡树时,不需要用标准 rbtree/avl 删除一个节点每次再平衡的传统方法,可以使用一种类似“摘叶子”的方法解构二叉树,每次选择最近的叶子节点删除,没有就往上回溯父节点,比标准方法老老实实删除快很多。
比如传统二叉树的增删改查都是要比较键值的,而比较键值是个很费时间的操作(比如用字符串做键值时),但是既然我们有哈希值,节点又是 unordered 的,那么在操作二叉树时,我们线比较哈希值,先用哈希值的大小进行比较,哈希值相同了再实际比较键值,这样可以大大避免频繁的键值比较,最终每个节点大部分只有1次键值比较,少部分有2次以上比较。
。。。。
基准测试
引入一个新技术再大部分情况下如果比老技术更慢就别玩了,不能光说不练嘛,我们测试一下上面说的这些方法最终效果如何。首先看看正常情况下,即 hash 值均匀分布的情况下它的表现,对比的是几个主流编译器自带的 STL 里的 unordered_map,为了避免额外因素干扰,两边都用 int 值做主键,使用了相同的哈希函数:hash(x) = x,这也是大部分 STL 实现默认的 hash函数:

上面的 avl-hash 是我们上面实现的树表混合结构,二叉平衡树我用的是 AVL,这是个人习惯问题了,关于 avl / rbtree 的性能其实是差不多的,我以前讨论过,这里不展开了:
韦易笑:AVL树,红黑树,B树,B+树,Trie树都分别应用在哪些现实场景中?
你也可以用 rbtree 代替,这里纯粹一个个人口味问题,下面比较了 Windows / Linux 下面vc和 gcc 自带的 std::unordered_map ,从查询时间看,两个差不多,avl-hash 略微领先一些,后面插入时间和删除时间 std::unordered_map 很吃亏,因为我们的树表混合结构里自己管理了节点内存分配,而 unordered_map 却使用了默认内存分配器(会用系统默认的内存分配),所以排除内存分配开销,二者差距应该没上面那么大,比如 ubuntu 下面 libc 内存分配器对于 128 字节以内的对象分配直接使用 fastbin (一种freelist),性能比windows下的好很多,接近 avl-hash 内部自己管理内存的速度,因此性能差距会比 windows 小不少。
冲突测试
大部分哈希表都让用户 “选择一个合适的哈希函数”,而什么哈希函数才最合适?才分布最好?谁他妈都说不清,特别时对于未知键值到底会是怎样的情况下,你完全没根据去选择一个“好”的哈希函数,比如你给 python 重新设计一遍字典,你能预知成千上万用户会用它存什么吗?比如你实现一个 redis / mq 之类的服务,你知道用户会发送什么键值上来?而这类服务,同一个哈希表里 hold 住百万级别的键值是很常见的事情。
未来键值不确定时,必须把希望寄托在一个“先验”的好的 hash函数上么?不需要了,这回我们可以靠哈希表自己了。前面实现了那么多,究竟我们实现的 “最不坏的哈希表”,不坏到什么程度?当发生碰撞时,或者 load-factor 比较高的情况下,性能是否能达到预期?
激动人心的时刻终于到了,第一项,搜索测试:

可以看出搜索对比,横轴表示冲突节点数量,纵轴表示测试耗时,可以看出随着碰撞的增加,树表混合结构的查询时间基本只是从 0毫秒增加到了 1-2毫秒,而 unordered_map 的搜索时间却是抛物线上升到1.4秒了。

插入和删除耗时类似

删除操作都比较费时,unordered_map 在三万个节点时基本接近1.6秒,而我们的树表混合结构耗时只有少许增加。
相关代码:https://github.com/skywind3000/avlmini
通过上面的工作,我们得到了这个最不坏的哈希表,我们用它做一个类似 redis / mq 的服务,存储百万级别的键值不用太过在意数据哈希值分布不均匀所带来的问题了,也不用担心碰撞攻击会让其性能跌落到深渊。
我们没法完全依赖哈希函数,当哈希函数靠不住时,还得靠哈希表本身,这叫打铁还需自身硬嘛,最终测试基本符合我们的初衷和预期。
(完)